9 Mind Blowing Math Equations True Geeks Should Know!
For most of us, math equations are nothing but series of numbers we memorize just to pass an exam, and we usually forget all about them immediately. However, especially for mathematicians, they are almost like works of art. They derive aesthetic pleasure from their work, and from mathematics in general. Here are 11 examples to show you that math is actually really really cool!
1.

2.
6174 is known as Kaprekar's Constant after the Indian mathematician D. R. Kaprekar. This number is notable for the following property:
Take any four-digit number, using at least two different digits. (Leading zeros are allowed.)
Arrange the digits in descending and then in ascending order to get two four-digit numbers, adding leading zeros if necessary.
Subtract the smaller number from the bigger number.
Go back to step 2.
The above process, known as Kaprekar's Routine, will always reach its fixed point, 6174, in at most 7 iterations. Once 6174 is reached, the process will continue yielding 7641 – 1467 = 6174. For example, choose 3524:
5432 – 2345 = 3087
8730 – 0378 = 8352
8532 – 2358 = 6174
7641 – 1467 = 6174
The only four-digit numbers for which Kaprekar's Routine does not reach 6174 are repdigits such as 1111, which give the result 0000 after a single iteration. All other four-digit numbers eventually reach 6174 if leading zeros are used to keep the number of digits at 4.
3.

4.

The Fibonacci Sequence is the series of numbers like 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, … The next number is found by adding up the two numbers before it.
If we tabulate these numbers in a column, shifting the decimal point one place to the right for each successive number, the sum equals 1/89. It's an instance of an interesting general pattern involving geometrically weighted sums of the terms of arbitrary linear recurring sequences.
5.

6.
A Knight's Tour is a sequence of moves of a knight on a chessboard such that the knight visits every square only once. If the knight ends on a square that is one knight's move from the beginning square (so that it could tour the board again immediately, following the same path), the tour is closed, otherwise, it is open.
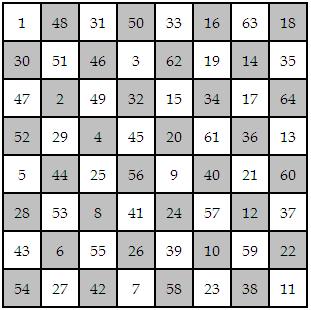
The Knight's Tour problem is the mathematical problem of finding a knight's tour. In the table, “1” is the beginning point. As you can see, each of the columns adds up to 260! And each half-row and half-column sum to 130.
7.

8.
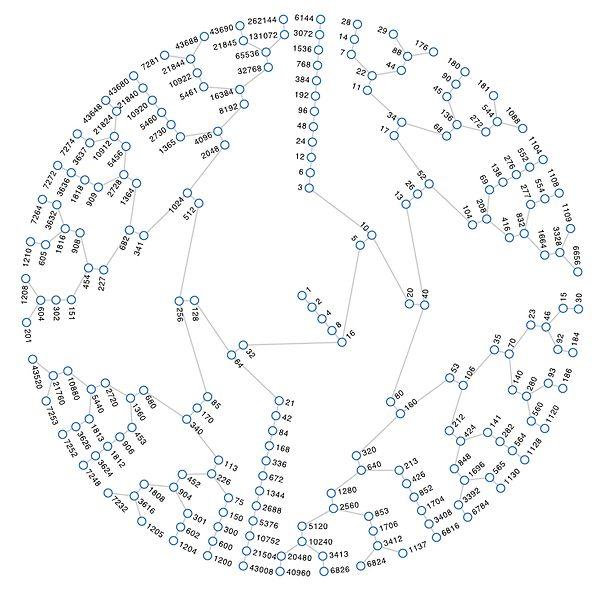
The Collatz Conjecture is a conjecture in mathematics named after Lothar Collatz. The conjecture is also known as the 3n + 1 conjecture, the sequence of numbers involved is referred to as the hailstone sequence or hailstone numbers (because the values are usually subject to multiple descents and ascents like hailstones in a cloud). The conjecture can be summarized as follows. Take any positive integer n. If n is even, divide it by 2 to get n / 2. If n is odd, multiply it by 3 and add 1 to obtain 3n + 1. Repeat the process indefinitely. The conjecture is that no matter what number you start with, you will always eventually reach 1.
9.

142857 is the best-known cyclic number in base 10. If it is multiplied by 2, 3, 4, 5, or 6, the answer will be a cyclic permutation of itself, and will correspond to the repeating digits of 2/7, 3/7, 4/7, 5/7, or 6/7 respectively.
1 × 142,857 = 142,857
2 × 142,857 = 285,714
3 × 142,857 = 428,571
4 × 142,857 = 571,428
5 × 142,857 = 714,285
6 × 142,857 = 857,142
7 × 142,857 = 999,999
(If you multiply by an integer greater than 7, there is a simple process to get to a cyclic permutation of 142857.)
10.

This magic square has 24 groups of four fields with the sum of 139 and in the first row - shown at bottom-right - The Indian mathematician Srinivasa Ramanujan's date of birth: December 22, 1887.
11.
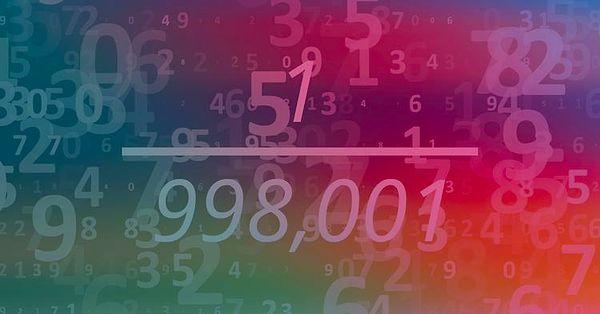
If you divide 1 by 998,001, the resulting decimal number will give you almost every three digit number. For example, the decimal starts as follows: 0.000001002003004005006... and so on.
Almost, because one three digit number gets skipped: 998.
Keşfet ile ziyaret ettiğin tüm kategorileri tek akışta gör!


Send Comment